4.5 Graphs of Sine and Cosine Functions

The graph of a sine function is called a sine curve. The following graph represents one cycle of the sine curve and following that is the graph of the cosine function.

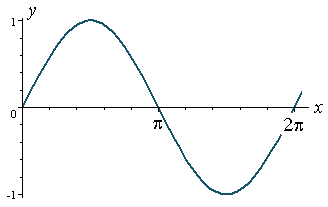
y= sin(x)

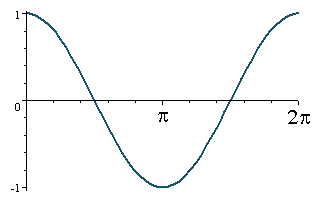
y= cos(x)

The domain of the sine and cosine functions is all real numbers, the range is [-1,1] and each function has a period of 2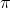

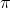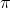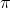Divide the period 2 to get 4 equal points: /2, , 3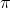/2, and 2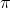

Using Key Points to Sketch a Sine Curve:

y= 2 sin(x)

These key points will have twice the magnitude of the graph y= sin(x)

(0,0) (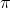/2, 2) (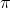, 0) (3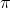/2, -2) (2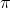, 0)

Amplitude and Period of Sine and Cosine Functions:

y= d + a sin(bx-c)

and

y= d + a cos(bx-c)

= amplitude of the function y= a sin(x) and y= a cos(x)

amplitude is half the distance between the maximum and minimum values of the function

ex. if y= 1/2 cos(x) the amplitude is 1/2, the maximum value is 1/2, and the minimum value is -1/2.

Divide one cycle, , into 4 equal parts to get the key points:

(0, 1/2) (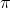/2, 0) (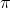, -1/2) (3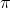/2, 0) (2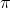, 1/2)

Period=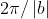

For the rest of the translations of sine and cosine curves, consider reviewing the transformations studied in section 1.3 in our blog:

y= f(x)

y= f(x)+2 shifts up 2

y= f(x+2) shifts left 2

y= f(x-2) shifts right 2

y= 2f(x) vertically stretched

y= (2x) horizontally compressed

y= -f(x) reflects in y-axis

y= f(-x) reflects in x-axis