We will begin discussing this section with the equation that Mr. Wilhelm showed us in class today, which read that a polynomial function is of the form:
There are two unfamiliar variables in play here: a and n.
The value of n must be a nonnegative number.
n can be:
- a whole number,
- equal to zero
- or a positive integer.
Another important part a polynomial function is its degree. Each polynomial function has a specific degree that is determined by the highest value for n where
For example, if =3x^{2}-5x+1) , the degree of this function is 2. This is because the x is raised to the second power, which is the highest value for n in this function.
, the degree of this function is 2. This is because the x is raised to the second power, which is the highest value for n in this function.
Let's try another. If =(3x^{2}-5x+1)(x^{2}-3)) , what is its degree? The correct answer is 4. Did I trick you? If you properly foil out this function, you will see that when
, what is its degree? The correct answer is 4. Did I trick you? If you properly foil out this function, you will see that when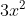 is distributed to
is distributed to 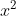 ,
,  is created! Eureka! Therefore, because
is created! Eureka! Therefore, because has the highest value for n at 4, the degree is 4.
has the highest value for n at 4, the degree is 4.
Now that we know what a polynomial function consists of, lets take a look at what its called. The chart below has three categories, Degree, Name, and Example.
Degree Example Name
0 =1) Constant
Constant
1 =x+1) Linear
Linear
2 =2x^{2}+3x+4) Quadratic
Quadratic
3 =x^{3}) Cubic
Cubic
4 =4x^{4}-1) Quartic
Quartic
Now, let's go more in depth into a very widely-used polynomial function, the quadratic.
The basic formula for a quadratic is 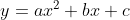 , where a, b and c are the coefficients. An example graph of this is:
, where a, b and c are the coefficients. An example graph of this is:
in which  . It is important to note that the quadratic formula is very helpful here:
. It is important to note that the quadratic formula is very helpful here:
The two x-intercepts can be found by using the quadratic formula. The intercept farthest to the right will use -b+ while the intercept farthest to the left will use -b-.
This quadratic graph has an axis of symmetry traveling down what would be the line of x=3.
At the bottom tip of the quadratic, located at the point
(3,-2), lies the vertex. In this case, the vertex of the graph is the minimum. In order to find the x coordinate of the vertex, you can use 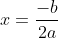 .
.
Another way to look at the equation of a quadratic polynomial is to use the vertex equation. The vertex equation is: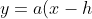^{2}+k) in which the vertex is simply at (h, k). In the case of the graph above, the vertex equation is
in which the vertex is simply at (h, k). In the case of the graph above, the vertex equation is
The last topic that we will discuss is how to change a normal quadratic equation to a vertex equation. A reason we should know this is that it is easier to find the vertex on a graph using the vertex equation than with the normal quadratic equation. The best way to approach this is by using completing the square.
We will go through this process using four easy steps.
1. When starting with a quadratic equation, such as =x^{2}+6x+5) , it is important to isolate c. Here, we will isolate 5. So just for now, move the 5 to a far off space on your page. Just forget about it.
, it is important to isolate c. Here, we will isolate 5. So just for now, move the 5 to a far off space on your page. Just forget about it.
2. Add ^{2}) to
to  . We are doing this so that we will be able to factor easily later on. Here, we will add 9. But it's not that simple; we can't just add blindly! In order to successfully add 9, we will need to subtract 9 from something else.
. We are doing this so that we will be able to factor easily later on. Here, we will add 9. But it's not that simple; we can't just add blindly! In order to successfully add 9, we will need to subtract 9 from something else.
3. Remember that 5? You know, the one I told you to forget about? We now need to subtract 9 from the 5 to make it -4. Now, the equation should look like this:
4. The last step is to factor your new
And thats it! We have successfully changed a quadratic equation into a vertex equation! Hold on, I have one last question for you to make sure you were reading: what is the vertex of the function we just made? The correct answer is (-3, 4).
Thanks for reading!


No comments:
Post a Comment