2.6: Rational Functions and Asymptotes

Section 2.6 is an introduction to rational functions.

The definition of a rational function is: "any function which can be written as the ratio of two polynomial functions."

According to our book, a rational function can be written in the form

where N(x) and D(x) are polynomials and D(x) is not the zero polynomial.

We learned form Chapter 1 that the domain of a rational function of x includes all real numbers except x-values that make the denominator zero.

The other topic of 2.6 is asymptotes.

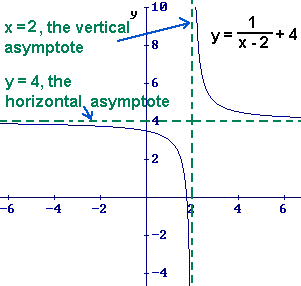
The definition of a vertical asymptote is "A vertical line which the graph of the line of a function approaches but never reaches."

The definition of a horizontal asymptote is "A horizontal line which the graph of a function approaches as variable tends to positive or negative infinity. It should be noted that the graph can cross the horizontal asymptote as many times as it likes (as with many oscillating functions). A horizontal asymptote occurs when the limit of a function as the variable approaches either positive or negative infinity is a constant."

Let "f" be the rational function f(x) where

where

N(x) = a_nxⁿ + a_n-1x^n-1 + ... + a₁x + a₀ and

D(x) = b_mx^m + b_m-1x^m-1 + ... + b₁x + b₀

Where N(x) and D(x) have no common factors.
1. The graph of "f" has vertical asymptotes at the zeros of D(x).
2. The graph of "f" has at most one horizontal asymptote determined by comparing the degrees of N(x) and D(x).
a. If n is less than m, the line y = 0 (x-axis) is a horizontal asymptote.
b. If n = m, the line is a horizontal asymptote.

c. If n is greater than m, the graph of "f" has no horizontal asymptote.

Example: Find the Domain and Asymptotes

1. Find the vertical asymptotes by taking D(x) and setting it equal to zero.

(x - 2)³ = 0
x - 2 = 0
x = 2

therefore a vertical asymptote is the line x = 2

2. Find the horizontal asymptotes
n = 0 and m = 3 so n is less than m, therefore the line y = 0 is the horizontal asymptote.

3. Graph it using a graphing utility.

4. Domain (- ∞, 2) U (2, ∞)

5. Range (- ∞, 0) U (0, ∞)

The x-intercepts are where the graph crosses the x-axis, and the y-intercepts are where the graph crosses the y-axis.

More specifically,

• an x-intercept is a point in the equation where the y-value is zero, and
• a y-intercept is a point in the equation where the x-value is zero.
  

• Find the x- and y-intercepts of 25x² + 4y² = 9

Using the definitions of the intercepts, I will proceed as follows:

x-intercept(s):

y = 0 for the x-intercept(s), so:

25x² + 4y² = 9
25x² + 4(0)² = 9
25x² + 0 = 9
x² =


x = ± ( )




Then the x-intercepts are the points (, 0) and ( , 0)

y-intercept(s):

x = 0 for the y-intercept(s), so:

25x² + 4y² = 9
25(0)² + 4y² = 9
0 + 4y² = 9
y² =


y = ± ( )

Then the y-intercepts are the points (0, ) and (0, )

Just remember: Whichever intercept you're looking for, the other variable gets set to zero.