For example in the set of numbers below, every domain is only paired with one range, making it a true function (more can be read in the previous blog post about functions).
{(2,3),(3,4),(5,6),(4,3)} <---- notice how every x value has only 1 value for y. Even though the value 3 is the value for two separate x values, each domain has only one range which can be the same as other ranges.
=3x^{2}+4)
=3\left%20(%202%20\right%20)^{2}+4)
=%203(4)+4)
=%2012+4)
=%2016)
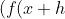-f(x))/h)
=2x+5)
+5-2x+5)/h)
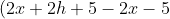/h)

In a function, the domain or input is set up as the function of the input or otherwise written as f(x) or f of x. This implies that for whatever value for x that is the input, there will be an output as a result of the function.
In simpler terms, this means for whatever x equals (a number, another value, an equation) you can substitute that value into the equation where x is prevalent.
For example,
This simply states that the function of x or f(x) equals 3 times the value of whatever 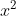 is, plus 4.
is, plus 4.
If we take the domain (x) and assign a value to it:
x=2
We can take that value and substitute it into the equation.
This simply states that for the function or value of 2, it is input into the equation for the value of x. We then simplify.
Simplify.
Simplify.
This final statement says that for the input or domain of 2 into the function, the value it is paired with is 16.
Difference Quotient
The difference quotient is simply a function used in pre-calculus and calculus. It is described as such where the domain is an equation as the value.
Here's the difference quotient:
Lets say that
Because for the value of the domain x equals 2x+5, we substitute
If we distribute the 2 and the negative in the equation (remember it was a -f(x) in the original function...
Simplified.
This simplifies right into the answer of 2.
Here's a video that may help explain with more examples:
No comments:
Post a Comment