We all have learned the basic of functions at this point so know we're going to take it to a new level. next we're going to try combining them. in this blog I'll show you 4 of the five basic ways to do this. starting with the basic function f(x)=2x-3 and g(x)=x^2 -1. now remember these functions because we're going to come back to them quite a lot.
1.)We'll start with the sum of two functions. taking our to functions f(x) and g(x) we are going to create (f+g)(x) this is like saying f(x) + g(x) but you must write it as the first example as to avoid confusion.
lets start.
You've got your function? f(x)=2x-3 and g(x)=x^2 -1? now add them like this...
(f+g)(x)=(2x-3) + (x^2 -1) simply
=x^2 + 2x - 4
here a a few more example just in case your still shaky...
starting with f(x)= 2x-1 and g(x)= x^2 + 2x -1 add...
(f+g)(x)= f(x)+ g(x)
=(2x-1) + (x^2 + 2x -1) simply
=x^2 + 4x
Starting with f(x)= x^3+8 and g(x)= x+1 add...
(f+g)(x)= f(x) + g(x)
=(x^3+8) + (x+1)
=x^4 + x^3 + 8x + 9
2.)Now for finding the difference (aka. subtracting) going back to our two orignal fuctions f(x) and g(x) we are going to create (f-g)(x) this is like saying f(x) - g(x).
OK, You've got your function? f(x)=2x-3 and g(x)=x^2 -1? now subtract them like this...
(f-g)(x)=(2x-3) - (x^2 -1) simply
=-x^2 + 2x - 2
And now for so more examples....
starting with h(x)= x^2-4 and j(x)= x^2 + 3x
(h-j)(x)=(x^2-4)-(x^2 +3x)
=x^2-4-x^2-3x
=3x-4
Starting with k(x)=3x+7 and d(x)= x^2 -3
(k-d)(x)=(3x+7)-(x^2-3)
=3x+7-x^2+3
=-x^2+3x+10
3.) Now we'll find the Product of two functions or in other words well multiply them.
back to our functions f(x) and g(x) we're going to find (fg)(x) or f(x) * g(x)...
take (fg)(x)=(2x-3)(x^2-1)
=2x^2 - 3x^2 - 2x + 3
More examples...
Starting with t(x)=x^2 and u(x)= x -3
(tu)(x)=(x^2)(x-3)
=x^3 - 3x^2
4.) and finally finding the quotient or dividing the functions. we're going to take f(x) and g(x) and make (f/g)(x) or f(x)/g(x).
Take (f/g)(x)=(2x-3)/(x^2-1)
for these that's all you need to do however typically because of how simple that is people might ask you to find the domain...
on this example it would be x =/= ±1
more examples...
starting with w(x)=√x and y(x)=√4-x^2
(w/y)(x)= (√x)/(√4-x^2)
the domain would be (w/y)(x) would be [0,2)
Thursday, December 15, 2011
Wednesday, December 14, 2011
Section 1.3: Shifting, Reflecting, and Stretching Graphs
Shifting, reflecting, and stretching graphs may seem pretty strait forward at first but there are a few things to keep in mind to prevent confusion.
But before we get ahead of ourselves, let's begin with the parent functions.
Parent functions are "a set of basic functions used as building blocks for more complicated functions." (Mathwords)
Examples of these parent functions are:


As you can see these graphs touch the origin and are not stretched, compressed, or flipped in any way.
But now let's move away from the parent functions. We'll start with something simple like shifting the graph of \[f(x)=x^2\] along the y-axis using the equation \[f(x)=x^2-2\].

But before we get ahead of ourselves, let's begin with the parent functions.
Parent functions are "a set of basic functions used as building blocks for more complicated functions." (Mathwords)
Examples of these parent functions are:


As you can see these graphs touch the origin and are not stretched, compressed, or flipped in any way.
But now let's move away from the parent functions. We'll start with something simple like shifting the graph of \[f(x)=x^2\] along the y-axis using the equation \[f(x)=x^2-2\].

Seems pretty strait forward, right? You subtract 2 from \[x^2\] and the y-coordinate of the vertex moves down 2. If you were to add 2, it would move up 2. Simple enough.

Now you may be thinking something along the lines of "If we subtracted 2 from \[x\], why did the graph move to the right?" That's the counter-intuitive part I was talking about. When you subtract from \[x\] the graph moves to the right and when you add to \[x\] the graph moves to the left.
If you would prefer to just memorize the above fact then, by all means, go right ahead. If you would like an explanation, I've got one. Since the graph is only moving along the x-axis the value of the y-coordinate (\[f(x)\]) will always equal \[0\].
Using this information we get that \[0=(x-2)^2\]. Now it comes down to basic Algebra.
This same counter-intuitiveness applies to stretching and compressing. It makes sense that multiplying a function by 2 would make its graph wider and multiplying that same function by \frac{1}{2} would make it more narrow. However, the oposite of this is true. Multiplying a function by 2 makes its graph more narrow and multiplying that same function by \frac{1}{2} would makes it wider.
The best way to understand this is to see it in the actual graph.
 As you can see the function \[f(x)=2x^2\] (the green graph) is more narrow than its parent function. This is because the function's outputs increase more quickly than the parent function. The same principle applies with the function \[f(x)=\frac{1}{2}x^2\] (the blue graph). It is wider because it's outputs increase slower than the parent function.
As you can see the function \[f(x)=2x^2\] (the green graph) is more narrow than its parent function. This is because the function's outputs increase more quickly than the parent function. The same principle applies with the function \[f(x)=\frac{1}{2}x^2\] (the blue graph). It is wider because it's outputs increase slower than the parent function.
Now we move on to reflections. We will be using a cubic function for this part because it will better illustrate the results of the reflection.
To get a reflection in the x-axis all you have to do is take the function (in this case \[f(x)=2x^3-3x^2-4x \]) and multiply it by -1. It should look like this: \[f(x)=-1(2x^3-3x^2-4x)\]

But what if you want something reflected in the y-axis? All you have to do is have the function be \[f(-x)\]. In this case that would be \[f(-x)= 2(-x)^3-3(-x)^2-4(-x)\]

But what if you want to move it along the x-axis? This is where things get a little counter-intuitive. Before we worry about that, we need to figure out how to move it along the x-axis to begin with.
To move the graph vertically we subtracted 2 after squaring \[x\]. To move the graph horizontally we have to subtract 2 from \[x\] then square it. You can see this in the equation .
.
 .
.
Now you may be thinking something along the lines of "If we subtracted 2 from \[x\], why did the graph move to the right?" That's the counter-intuitive part I was talking about. When you subtract from \[x\] the graph moves to the right and when you add to \[x\] the graph moves to the left.
If you would prefer to just memorize the above fact then, by all means, go right ahead. If you would like an explanation, I've got one. Since the graph is only moving along the x-axis the value of the y-coordinate (\[f(x)\]) will always equal \[0\].
Using this information we get that \[0=(x-2)^2\]. Now it comes down to basic Algebra.
This same counter-intuitiveness applies to stretching and compressing. It makes sense that multiplying a function by 2 would make its graph wider and multiplying that same function by \frac{1}{2} would make it more narrow. However, the oposite of this is true. Multiplying a function by 2 makes its graph more narrow and multiplying that same function by \frac{1}{2} would makes it wider.
The best way to understand this is to see it in the actual graph.
 As you can see the function \[f(x)=2x^2\] (the green graph) is more narrow than its parent function. This is because the function's outputs increase more quickly than the parent function. The same principle applies with the function \[f(x)=\frac{1}{2}x^2\] (the blue graph). It is wider because it's outputs increase slower than the parent function.
As you can see the function \[f(x)=2x^2\] (the green graph) is more narrow than its parent function. This is because the function's outputs increase more quickly than the parent function. The same principle applies with the function \[f(x)=\frac{1}{2}x^2\] (the blue graph). It is wider because it's outputs increase slower than the parent function.Now we move on to reflections. We will be using a cubic function for this part because it will better illustrate the results of the reflection.
To get a reflection in the x-axis all you have to do is take the function (in this case \[f(x)=2x^3-3x^2-4x \]) and multiply it by -1. It should look like this: \[f(x)=-1(2x^3-3x^2-4x)\]

But what if you want something reflected in the y-axis? All you have to do is have the function be \[f(-x)\]. In this case that would be \[f(-x)= 2(-x)^3-3(-x)^2-4(-x)\]

Tuesday, December 13, 2011
Graphs of Functions 1.2
Finding the Domain and Range of a Function
Domain: all possible x-coordinates of a graph
Range: all possible y-coordinates of a graph
Finding Domains:
Find the domain of y=x²+x+2
Domain: all possible x-coordinates of a graph
Range: all possible y-coordinates of a graph
Finding Domains:
Find the domain of y=x²+x+2
- The domain for this equation would be (-∞,∞) because this equation can be any real number in order to remain a function
Find the domain of y=√(x²-4)
- When you have a square root the number inside the radical can't be negative, otherwise it will result in an imaginary number.
- Pretend like the radical isn't there
- set y=0 so you have x²-4=0
- x=±2
- It's okay for the number under the radical to be zero, but it is not okay for the number under the radical to be negative because that would result in an imaginary number. We know that both 2 and -2 equal zero. By testing out numbers on the number line we find that any number in between -2 and 2 would make the number under the radical negative (not including 2 and -2).
- By this we can tell that all possible domains for this function will be: [-∞,-2) U [2,∞)
Find the domain of the Function: ( x+4)/(x²+3x+2)
- In this Equation for finding the domain the numerator does NOT matter
- Factor the denominator
- x=-2 and -1
- The only restrictions are that the denominator can't be 0.
- The domain of this function is: (-∞,-2) U (-1,∞)
Finding the Range:
Find the Range of the Function: y=x²+2x+1
- We know that this equation is going to be a parabola pointing downward. Therefore this parabola is going to have a minimum range
- By finding the vertex for x, x = -b/2a we will get an answer of -1 to find the minimum value we plug -1 back into the equation and we get 0.
- Since the graph has a minimum the answer for all range values is going to be bigger than 0
- The range for this function is [0,∞)
Increasing and Decreasing Functions
- A function f is increasing on an interval if the slope of the interval is positive.
- A function f is decreasing on an interval if the slope of the interval is negative.
- A function f is constant on an interval if the slope of the graph is a horizontal line.
Even and Odd Functions
- A function is even if f(-x)=f(x). You can tell if a graph is even if it is symmetrical through the y-axis
- A function is odd if f(-x)=-f(x). You can tell if a graph is odd if it is symmetrical through the origin
Monday, December 12, 2011
Wednesday, December 7, 2011
Domain and Difference Quotient
"The domain of a function is the set of all values of the independent variable for which the function is defined" (Visual Calculus). The domain also is known as the input which in variable terms can be anything, but is usually described as (x). For every domain, there is also a rule that only 1 value can be the range or output.
For example in the set of numbers below, every domain is only paired with one range, making it a true function (more can be read in the previous blog post about functions).
{(2,3),(3,4),(5,6),(4,3)} <---- notice how every x value has only 1 value for y. Even though the value 3 is the value for two separate x values, each domain has only one range which can be the same as other ranges.
=3x^{2}+4)
=3\left%20(%202%20\right%20)^{2}+4)
=%203(4)+4)
=%2012+4)
=%2016)
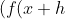-f(x))/h)
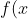=2x+5)
+5-2x+5)/h)
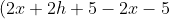/h)

In a function, the domain or input is set up as the function of the input or otherwise written as f(x) or f of x. This implies that for whatever value for x that is the input, there will be an output as a result of the function.
In simpler terms, this means for whatever x equals (a number, another value, an equation) you can substitute that value into the equation where x is prevalent.
For example,
This simply states that the function of x or f(x) equals 3 times the value of whatever 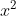 is, plus 4.
is, plus 4.
If we take the domain (x) and assign a value to it:
x=2
We can take that value and substitute it into the equation.
This simply states that for the function or value of 2, it is input into the equation for the value of x. We then simplify.
Simplify.
Simplify.
This final statement says that for the input or domain of 2 into the function, the value it is paired with is 16.
Difference Quotient
The difference quotient is simply a function used in pre-calculus and calculus. It is described as such where the domain is an equation as the value.
Here's the difference quotient:
Lets say that
Because for the value of the domain x equals 2x+5, we substitute
If we distribute the 2 and the negative in the equation (remember it was a -f(x) in the original function...
Simplified.
This simplifies right into the answer of 2.
Here's a video that may help explain with more examples:
Tuesday, December 6, 2011
December 6: Introduction to Functions
Section 1.1 is an introduction to functions. A function, according to our textbook is "... a set A to a set B is a relation that assigns to each element x in the set A exactly one element y in the set B. The set A is the domain (or set of inputs) of the function f, and the set B contains the range (or set of outputs).
Simplified, this means that a function is a relationship between two things in which for every x value (the input) there is only one y value (the output).
For example, the relationship between the side length of a square and its area is a function. The reasoning behind this is that every square that has the same side length will have the same area. (The input, in this case the side length will always have the same single output, in this case- the area)
Simplified, this means that a function is a relationship between two things in which for every x value (the input) there is only one y value (the output).
For example, the relationship between the side length of a square and its area is a function. The reasoning behind this is that every square that has the same side length will have the same area. (The input, in this case the side length will always have the same single output, in this case- the area)
The relationship between the height of a rectangle and the area of a rectangle, though, is not a function. In this example, the area depends upon the width of the rectangle for the area, not just the height. Let’s say that one rectangle’s height is 3 and the width is 5, then that rectangle’s area is 15. If the second rectangle’s height is still 3 but it has a width of 7, then its area will be 21 not 15. That means that the input (3), has more than just one output.
However, a function is still a function if an output has more than one input. For example, the set of points: {(-5,2), (-2, 1), (0,0), (3,7), (4,2)} is a function even though the -5, and 4 both result in 2.
A set of points that is not a function is: {(-5,2), (-2, 1), (0,0), (3,7), (4,2), (3,-3)} because one element in the domain, 3, corresponds with more than one range 7 & -3.
Today, we also talked about Function Notation or f (x)
For example:
Then...
f (2)=2(2)+ 1=5
and
f (a)= 2(a) +1
and
f (!)=2(!) +1
* All these examples are assuming that y (the output) is a function of x (the input).
Wednesday, November 30, 2011
Chapter P
Sections P.4 and P.5 were review of topics, mostly from Algebra 2, with which you should be familiar. Section P.4 focused on solving equations of many types. The ones we spent the most time with were equations involving fractions and radical expressions.
Perhaps the easiest way to solve an equation with rational expressions (i.e., fractions) is to multiply both sides of the equation by the least common multiple of all the denominators. Multiplying through will eliminate all the denominators, so there will be no fractions remaining. From there, the equation will usually be either quadratic or linear and should be relatively straightforward to solve. Remember to check that none of your solutions make any denominator in the original equation equal zero.
When a variable is under a radical, both sides of the equation will need to be squared. Before doing this, isolate the radical term. (When there are two radical terms, it is typically easier to separate them before squaring both sides for the first time.) After squaring both sides of the equation, you will usually be left with a quadratic or linear equation to solve. Remember to check for extraneous solutions! When you square both sides of an equation, you open the door to extraneous solutions, so you have to check them by plugging them into the original equation.
P.5 dealt primarily with absolute value and inequalities.
Definition of absolute value:
|x| = a if and only if x = a or - x = a
for inequalitites:
|x| < a if and only if x < a or - x < a
Example:
Once the absolute value expression is isolated on one side of the inequality sign, split the problem into two separate inequalities (based on the definition above).

Polynomial inequalities are a big part of P.5. Solving them is more complicated than solving equations.
Before the official solving begins, you must have a zero on one side of the inequality.
The first to solve a polynomial inequality is to find the zeros of the polynomial.
Use these zero to set up intervals, and then pick a test value in each interval.
Plug each test value into the polynomial and see if its value is positive or negative.
Your solution will include all the intervals that matched your inequality (+ for >0 and - for <0).
This process makes more sense when you consider the graph of your inequality. The inequality is >0 when its graph is above the x-axis and <0 when its graph is below the x-axis. Setting up the test intervals is a numeric way of making that determination.
Example:
The first order of business is to find the zeros of the polynomial.
Perhaps the easiest way to solve an equation with rational expressions (i.e., fractions) is to multiply both sides of the equation by the least common multiple of all the denominators. Multiplying through will eliminate all the denominators, so there will be no fractions remaining. From there, the equation will usually be either quadratic or linear and should be relatively straightforward to solve. Remember to check that none of your solutions make any denominator in the original equation equal zero.
When a variable is under a radical, both sides of the equation will need to be squared. Before doing this, isolate the radical term. (When there are two radical terms, it is typically easier to separate them before squaring both sides for the first time.) After squaring both sides of the equation, you will usually be left with a quadratic or linear equation to solve. Remember to check for extraneous solutions! When you square both sides of an equation, you open the door to extraneous solutions, so you have to check them by plugging them into the original equation.
P.5 dealt primarily with absolute value and inequalities.
Definition of absolute value:
|x| = a if and only if x = a or - x = a
for inequalitites:
|x| < a if and only if x < a or - x < a
Example:

Using interval notation, we would represent our solution as [2,3].
Polynomial inequalities are a big part of P.5. Solving them is more complicated than solving equations.
Before the official solving begins, you must have a zero on one side of the inequality.
The first to solve a polynomial inequality is to find the zeros of the polynomial.
Use these zero to set up intervals, and then pick a test value in each interval.
Plug each test value into the polynomial and see if its value is positive or negative.
Your solution will include all the intervals that matched your inequality (+ for >0 and - for <0).
This process makes more sense when you consider the graph of your inequality. The inequality is >0 when its graph is above the x-axis and <0 when its graph is below the x-axis. Setting up the test intervals is a numeric way of making that determination.
Example:
The first order of business is to find the zeros of the polynomial.
Next, plot the zeros on a number line to establish the test intervals, then choose a test value from each interval. Plug that value into the polynomial and determine if the polynomial's value is postive or negative.
We were interested in where the polynomial was <0, so we choose the interval where f (x) was negative.
Using interval notation, we would express our solution as (3,5).
Below is the graph of the polynomial. Looking at that, it is clear that the interval where the graph is below the x-axis (<0) is from 3 to 5.
Subscribe to:
Comments (Atom)







