4.6 CSC, SEC, COT, and TAN Graphs
Let's start with the graph of

. We know that

translates to
 .
.
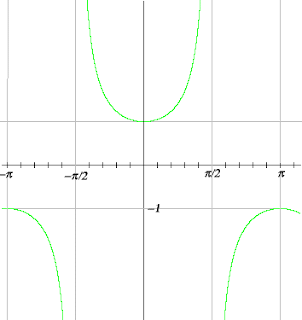
The graph of
 looks like this:
looks like this:
We can see that in this case, the graph will never cross the x-axis. This is because in order to find the
x-intercepts we need to set the numerator of the function,

, equal to zero. We know that 1 cannot be equal to zero, so there will be no x-intercepts. The asymptotes of the graph are

, and

, because the vertical asymptotes can be found by setting the denominator equal to zero, in this case

. By looking at the Unit Circle we can find out where

is zero, wherever the y-coordinate (which is equal to

), is zero.
Now let's move on to finding the graph of a

function.

is equal to

.
The graph of

looks like this:

The same things as with the

function apply. The x-intercepts are found by setting the numerator equal to zero, which in this case means there are no x-intercepts. The vertical asymptotes will be found by finding out where

equals zero. This again can be done by looking at where

is zero on the Unit Circle. And since

correlates to the y-coordinate,

is the x-coordinate. So wherever the x-coordinate is zero on the Unit Circle, is where the vertical asymptotes will be.
In this case they are at

, and

.
By now you can probably see how this works.

and

functions work much the same. Since

functions are the basis of

functions, let's look at

first.
The graph of a

function looks like this:
You can probably guess how we found the x-intercepts and the vertical asymptotes. X-intercepts are found when the numerator is set equal to zero, since

is equal to

, we can find the x-intercepts by finding out when

equals zero by looking at the unit circle.

equals zero at

and

, and so those are the x-intercepts. We do the same thing for finding the vertical asymptotes, except instead of looking at the numerator we look at where the denominator equals zero. The denominator (

) is zero at

, and

.
The

functions go the opposite way of

functions.

functions are

. Here's a graph of a

function:
As we can see, the graph goes down, instead of up like the

does. X-intercepts and vertical asymptotes are found exactly like those of all other functions- with the numerator and denominator.
An important thing to recognize about

and

functions is that their period is shorter than those
of

and

functions. The period of

and

functions is only

, not

. The formula is as follows:
All of the aforementioned functions undergo transformations. They may be stretched horizontally, or vertically. Or they may be compressed by a certain factor or shifted up/down a certain number. This all depends on what numbers affect the function.
Here's the basic formula of a function:

. 'trig' in this case is a placeholder for any of the trigonometric functions, (

,

,

,

,

and

).
Here is how it works:
- The value of a is the amplitude of the function. This means it tells us by how much the function is stretched or compressed vertically
- The value of b dictates the horizontal stretch/compression (remember that the effect it has becomes counter-intuative. If the value of b is greater than one, the curve will horizontally compress. If the value is less than one, it will horizontally stretch.)
- The value of c tells us if, and what, the horizontal shift is. This means that your graph may be moved to the left or right by whatever value c is.
- The value of d determines the vertical shift. This means that your graph may be moved up or down by whatever value d is.
 , or any other trigonometric function, we can see that the function is periodic, and therefore not one-to-one.
, or any other trigonometric function, we can see that the function is periodic, and therefore not one-to-one. , or any other trigonometric function, we can see that the function is periodic, and therefore not one-to-one.
, or any other trigonometric function, we can see that the function is periodic, and therefore not one-to-one.
 would appear like so:
would appear like so: would appear like so:
would appear like so: , The graph of
, The graph of  becomes becomes one-to-one, and therefore its inverse, shown below, is also a function.
becomes becomes one-to-one, and therefore its inverse, shown below, is also a function. , The graph of
, The graph of  becomes becomes one-to-one, and therefore its inverse, shown below, is also a function.
becomes becomes one-to-one, and therefore its inverse, shown below, is also a function.
 or
or  .
. or
or  .
. , but unlike the sine function, the domain of the cosine function is restrained to
, but unlike the sine function, the domain of the cosine function is restrained to  in order to maintain the function as one-to-one. The result is displayed below.
in order to maintain the function as one-to-one. The result is displayed below. , but unlike the sine function, the domain of the cosine function is restrained to
, but unlike the sine function, the domain of the cosine function is restrained to  in order to maintain the function as one-to-one. The result is displayed below.
in order to maintain the function as one-to-one. The result is displayed below.